type
Post
status
Published
date
Nov 24, 2022
slug
naive_bayes
summary
朴素贝叶斯(naive Bayes)法是基于贝叶斯定理与特征条件独立假设的分类方法。
tags
机器学习
数据分析
人工智能
Python
category
机器学习
icon
password
Property
Nov 24, 2022 12:54 PM
朴素贝叶斯(naive Bayes)法是基于贝叶斯定理与特征条件独立假设的分类方法。
朴素贝叶斯法
设输入空间\\(X\subseteq \mathbb{R}^n\\) 为\\(n\\) 维向量的集合,输出空间为类标记集合\\(Y=\{ c_1,c_2,...,c_K \}\\) ,输入特征向量\\(x \in X\\) ,输出类标记为\\(y\in Y\\) ,\\(P(X,Y)\\) 是\\(X\\) 和\\(Y\\) 的联合概率分布,数据集
$$T = \{ (x_1,y_1),(x_2,y_2),...,(x_n,y_n) \}$$
由\\(P(X,Y)\\) 独立同分布产生。
朴素贝叶斯法就是通过训练集来学习联合概率分布\\(P(X,Y)\\) .具体就是从先验概率分布和条件概率分布入手,俩概率相乘即可得联合概率。
称之为朴素是因为将条件概率的估计简化了,对条件概率分布作了条件独立性假设,这也是朴素贝叶斯法的基石,假设如下
$$P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k), k=1,2,...,K$$
这个公式在之前的假设条件下等价于
$$\prod \limits_{j=i}^n P(X^{(j)}=x^{(j)}|Y=c_k)$$
对于给定的输入向量\\(x\\) ,通过学习到的模型计算后验概率分布\\(P(Y=C_k|X=x)\\) ,后验分布中最大的类作为\\(x\\) 的输出结果,根据贝叶斯定理可知后验概率为
$$P(Y=c_k|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)}{\sum_kP(X=x|Y=c_k)P(Y=c_k)}$$
其中\\(\sum_kP(X=x|Y=c_k)P(Y=c_k)\Leftrightarrow P(X=x)\\)
所有\\(c_k\\) 的\\(P(X=x)\\) 都是相同的,这样我们可以把输出结果化简成
$$y = arg \max \limits_{c_k} P(Y=c_k) \prod_jP(X^{(j)}=x^{(j)}|Y=c_k)$$
这样,就了解了朴素贝叶斯法的基本原理了,下面要介绍的是参数估计。
参数估计
极大似然估计
我们已经知道对于给定的输入向量\\(x\\) ,其输出结果可以表示为
$$y = arg \max \limits_{c_k} P(Y=c_k) \prod_jP(X^{(j)}=x^{(j)}|Y=c_k)$$
可以使用极大似然估计法来估计相应的概率。先验概率\\(P(Y=c_k)\\) 的极大似然估计是
$$P(Y=c_k)=\frac{\sum \limits_{i=1}^NI(y_i=c_k)} {N}, k=1,2,...,K$$
设第\\(j\\) 个特征\\(x^{(j)}\\) 可能的取值的集合为\\( \{ a_{j1} ,a_{j2} ,...,a_{js_j} \}\\) ,条件概率\\(P(X^{(j)}=a_{jl}|Y=c_k)\\) 的极大似然估计是
$$P(X^{(j)}=a_{jl},Y=c_k)=\frac{\sum \limits_{i=1}^NI(x_i^{(j)}=a_{jl},y_i=c_k)} {\sum \limits_{i=1}^NI(y_i=c_k)}$$
$$j=1,2,...,n; l=1,2,...,S_j;k=1,2,...,K$$
学习与分类算法
下面给出朴素贝叶斯法的学习与分类算法。
算法 (朴素贝叶斯算法)
输入: 训练数据 \\(T = \{ (x_1,y_1),(x_2,y_2),...,(x_n,y_n) \}\\) , 其中\\(x_i = (x_i^{(1)},x_i^{(2)},...,x_i^{(n)} )^T\\) ,\\( x_i^{(j)}\in \{ a_{j1} ,a_{j2} ,...,a_{js_j} \}\\) ,\\(j=1,2,...,n\\) ,\\(l=1,2,...,S_j\\) ,\\(y_i \in \{ c_1,c_2,...,c_K \}\\);实例\\(x\\) ;
输出: 实例\\(x\\) 的分类.
(1) 计算先验概率及条件概率
$$P(Y=c_k)=\frac{\sum \limits_{i=1}^NI(y_i=c_k)} {N}, k=1,2,...,K$$
$$P(X^{(j)}=a_{jl},Y=c_k)=\frac{\sum \limits_{i=1}^NI(x_i^{(j)}=a_{jl},y_i=c_k)} {\sum \limits_{i=1}^NI(y_i=c_k)}$$
$$j=1,2,...,n; l=1,2,...,S_j;k=1,2,...,K$$
(2) 对于给定的实例\\(x = (x^{(1)},x^{(2)},...,x^{(n)} )^T\\) ,计算
$$P(Y=c_k) \prod_jP(X^{(j)}=x^{(j)}|Y=c_k),k=1,2,...,K$$
(3) 确定实例\\(x\\) 的类
$$y = arg \max \limits_{c_k} P(Y=c_k) \prod_jP(X^{(j)}=x^{(j)}|Y=c_k)$$
例子:试由下表的训练数据学习一个朴素贝叶斯分类器并确定\\(x=(2,S)^T\\) 的类标记,表中\\(X^{(1)},X^{(2)}\\) 为特征,\\(Y\\) 为类标记。
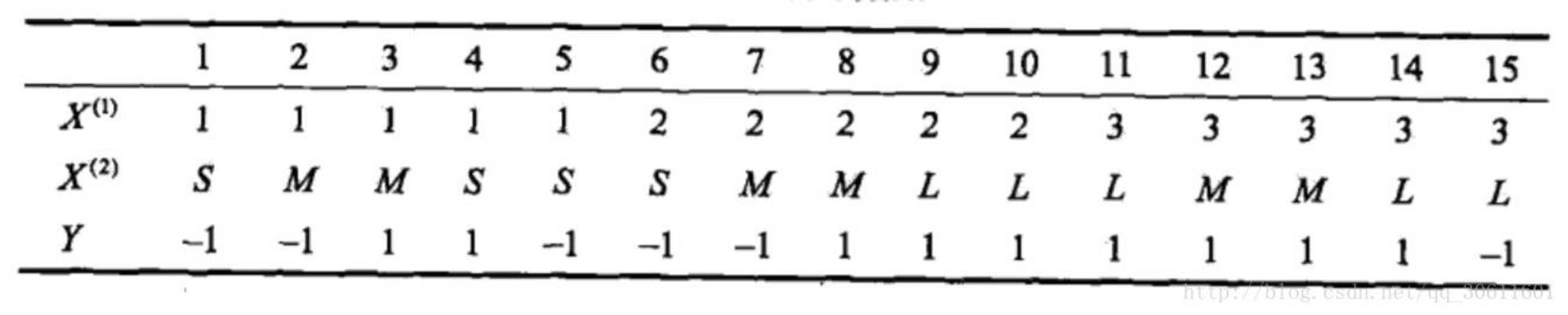
python代码如下:
import numpy as np #构造NB分类器 def Train(X_train, Y_train, feature): global class_num,label class_num = 2 #分类数目 label = [1, -1] #分类标签 feature_len = 3 #特征长度 #构造3×2的列表 feature = [[1, 'S'], [2, 'M'], [3, 'L']] prior_prob = np.zeros(class_num) # 初始化先验概率 con_prob = np.zeros((class_num,feature_len,2)) # 初始化条件概率 positive_count = 0 #统计正类 negative_count = 0 #统计负类 for i in range(len(Y_train)): if Y_train[i] == 1: positive_count += 1 else: negative_count += 1 prior_prob[0] = positive_count / len(Y_train) #求得正类的先验概率 prior_prob[1] = negative_count / len(Y_train) #求得负类的先验概率 ''' con_prob是一个2*3*2的三维列表,第一维是类别分类,第二维和第三维是一个3*2的特征分类 ''' #分为两个类别 for i in range(class_num): #对特征按行遍历 for j in range(feature_len): #遍历数据集,并依次做判断 for k in range(len(Y_train)): if Y_train[k] == label[i]: #相同类别 if X_train[k][0] == feature[j][0]: con_prob[i][j][0] += 1 if X_train[k][1] == feature[j][1]: con_prob[i][j][1] += 1 class_label_num = [positive_count, negative_count] #存放各类型的数目 for i in range(class_num): for j in range(feature_len): con_prob[i][j][0] = con_prob[i][j][0] / class_label_num[i] #求得i类j行第一个特征的条件概率 con_prob[i][j][1] = con_prob[i][j][1] / class_label_num[i] #求得i类j行第二个特征的条件概率 return prior_prob,con_prob #给定数据进行分类 def Predict(testset, prior_prob, con_prob, feature): result = np.zeros(len(label)) for i in range(class_num): for j in range(len(feature)): if feature[j][0] == testset[0]: conA = con_prob[i][j][0] if feature[j][1] == testset[1]: conB = con_prob[i][j][1] result[i] = conA * conB * prior_prob[i] result = np.vstack([result,label]) return result def main(): X_train = [[1, 'S'], [1, 'M'], [1, 'M'], [1, 'S'], [1, 'S'], [2, 'S'], [2, 'M'], [2, 'M'], [2, 'L'], [2, 'L'], [3, 'L'], [3, 'M'], [3, 'M'], [3, 'L'], [3, 'L']] Y_train = [-1, -1, 1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1] #构造3×2的列表 feature = [[1, 'S'], [2, 'M'], [3, 'L']] testset = [2, 'S'] prior_prob, con_prob= Train(X_train, Y_train, feature) result = Predict(testset, prior_prob, con_prob, feature) print('The result:',result) main()
得到结果:
The result: [[ 0.02222222 0.06666667] [ 1. -1. ]]
贝叶斯估计
极大似然估计的一个可能是会出现所要估计的概率值为0的情况,这时会影响到后验概率的计算结果,解决这一问题的方法是采用贝叶斯估计,具体的只需要在极大似然估计的基础上加多一个参数即可。
$$P_{\lambda}(X^{(j)}=a_{jl},Y=c_k)=\frac{\sum \limits_{i=1}^NI(x_i^{(j)}=a_{jl},y_i=c_k)+\lambda} {\sum \limits_{i=1}^NI(y_i=c_k)+S_j\lambda},\lambda \geq 0$$
当\\(\lambda=0\\) 时就是最大似然估计。常取\\(\lambda=1\\) ,这时称为拉普拉斯平滑(Laplace smoothing)。
小结
朴素贝叶斯法高效,且易于实现,但是其缺点就是分类的性能不一定很高。
参考文章
- Author:Quanfita
- URL:https://quanfita.cn/article%2Fnaive_bayes
- Copyright:All articles in this blog, except for special statements, adopt BY-NC-SA agreement. Please indicate the source!
Relate Posts
