type
Post
status
Published
date
Nov 24, 2022
slug
knn
summary
k近邻算法,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,就把该输入实例分类到这个类中。
tags
机器学习
数据分析
人工智能
Python
category
机器学习
icon
password
Property
Nov 24, 2022 12:58 PM
k近邻算法
k近邻算法,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,就把该输入实例分类到这个类中。
直接给出k近邻算法:
算法 (k近邻法)
输入: 训练数据集\\(T = \{ (x_1,y_1),(x_2,y_2),...,(x_n,y_n) \}\\), 其中\\(x_i \in X = \mathbb{R}^n,y_i \in Y = \{ c_1,c_2,...,c_K \},i = 1,2,...,N\\);实例特征向量\\(x\\);
输出: 实例\\(x\\)所属的类\\(y\\).
(1) 根据给定的距离度量,在训练集\\(T\\)中找到与\\(x\\)最邻近的\\(k\\)个点,蕴盖这\\(k\\)个点的\\(x\\)的邻域记作\\(N_k(x)\\);
(2) 在\\(N_k(x)\\)中根据分类决策规则(如多数表决)决定\\(x\\)的类别\\(y\\):
$$y=arg \max \limits_{c_j} \sum \limits_{x_i \in N_k(x)} I(y_i=c_i),i=1,2,...,N; j=1,2,...,K$$
其中,\\(I\\)为指示函数,即当\\(y_i=c_i\\)时\\(I\\)为1,否则\\(I\\)为0。
k近邻法没有显式的学习过程。
k近邻模型
k近邻算法使用的模型实际上对应于特征空间的划分,模型由三个基本要素——距离度量、k值的选择和分类决策规则决定。
距离度量
特征空间中俩个实例的距离是俩个实例点相似程度的反映,k近邻中一般使用欧氏距离。
设特征空间\\(X\\)是\\(n\\)维实数向量空间\\(\mathbb{R}^n\\),\\(x_i,x_j \in X,x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)})^T,x_j=(x_j^{(1)},x_j^{(2)},...,x_j^{(n)})^T\\),\\(x_i,x_j\\)的\\(L_p\\)距离为
$$L_p(x_i,x_j)= ( \sum \limits_{l=1}^{n} | x_i^{(l)}-x_j^{(l)} |^p )^{\frac{1}{p}}$$
$$p\geq 1\\)。
当\\(p=2\\)时,称为欧氏距离(Euclidean distance),即
$$L_2(x_i,x_j)= ( \sum \limits_{l=1}^{n} | x_i^{(l)}-x_j^{(l)} |^2 )^{\frac{1}{2}}$$
当\\(p=1\\)时,称为曼哈顿距离(Manhattan distance),即
$$L_1(x_i,x_j)=\sum \limits_{l=1}^{n} |x_i^{(l)}−x_j^{(l)} |$$
当\\(p=\infty \\)时,它是各个坐标距离的最大值,即
$$L_{\infty }(x_i,x_j)=\max \limits_{l} |x_i^{(l)}−x_j^{(l)} |$$
不同的距离度量所确定的最近邻点是不同的。
k值选择
k值得选择会对k近邻算法的结果产生重大影响!!!
如果选择的k值较小,就相当于用较小的的邻域中的训练实例进行预测。此时预测的结果会对近邻的实例点非常敏感。
如果选择较大的k值,就相当于在较大的邻域中训练实例进行预测。此时,与输入实例较远的训练实例也会对预测起作用,使预测发生错误。
如果k等于训练样本个数,此时将输入实例简单的预测为训练样本中最多的类。这时模型过于简单,会完全忽略训练样本中的大量有用信息,是不可取的。
在应用中,k值一般选取一个比较小的数值,通常采用交叉验证法来选取最优的k值。
分类决策规则
k近邻算法中分类决策规则往往是多数表决,即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类。
k近邻法的实现:kd树
kd树是一种对k维空间中的样本点进行存储以便对其进行快速检索的树形结构,它是一种二叉树,表示对k维空间的一个划分。构造k树相当于不断的用垂直于坐标轴的超平面去划分k维空间,构成一些列的k维超矩形区域,kd树的每个节点对应于一个k维的超矩形区域。
构造kd树
通俗来讲,对于一个样本空间的样本点,计算每一个维度的方差,按照方差最大的那个维度来排序,因为方差大代表的是数据分散的比较开,这样分割会有更高的分割效率。取中位数作为根节点,小于中位数的样本点作为左子树,大于的作为右子树。重复进行,直到得到一棵完整的二叉树。
算法 (构造平衡kd树)
输入:k维空间数据集\\(T= \{ x_1,x_2,...,x_N \}\\),其中\\(x_i = (x_i^{(1)},x_i^{(2)},...,x_i^{(k)})^T, i=1,2,...,N\\)
输出:kd树
(1) 开始:构造根节点,根节点对应于包含\\(T\\)的\\(k\\)维空间的超矩形区域。
选择中\\(x^{(1)}\\)为坐标轴,以\\(T\\)中\\(x^{(1)}\\)坐标的中位数作为且分点,将根节点对应的超矩形区域切分为两个子区域,切分面为垂直于\\(x^{(1)}\\)轴的平面。将落在切分面上的点作为根节点,左子节点为对应坐标\\(x^{(1)}\\)小于切分点的区域,右子节点为对应坐标\\(x^{(1)}\\)大于切分点的区域。
(2) 重复:对深度为\\(j\\)的节点,选择中\\(x^{(1)}\\)为切分的坐标轴,\\(l=j( \mod k )+ 1\\),以该节点的区域中所有实例的\\(x^{(l)}\\)坐标的中位数为切分点,将该节点对应的超矩形区域切分为两个子区域。
(3) 直到子区域内没有实例存在时停止。
例子 : 给定一个二维空间的数据集:\\(T= \{ (2,3)^T,(4,5) ^T,(9,6)^T,(4,7)^T,(8,1)^T,(7,2)^T \}\\)构造一个平衡kd树。(Wikipedia)
Python代码如下:
from collections import namedtuple from operator import itemgetter from pprint import pformat class Node(namedtuple('Node', 'location left_child right_child')): def __repr__(self): return pformat(tuple(self)) def kdtree(point_list, depth=0): try: k = len(point_list[0]) # assumes all points have the same dimension except IndexError as e: # if not point_list: return None # Select axis based on depth so that axis cycles through all valid values axis = depth % k # Sort point list and choose median as pivot element point_list.sort(key=itemgetter(axis)) median = len(point_list) // 2 # choose median # Create node and construct subtrees return Node( location=point_list[median], left_child=kdtree(point_list[:median], depth + 1), right_child=kdtree(point_list[median + 1:], depth + 1) ) def main(): point_list = [(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)] tree = kdtree(point_list) print(tree) if __name__ == '__main__': main()
我们得到以下结果:
((7, 2), ((5, 4), ((2, 3), None, None), ((4, 7), None, None)), ((9, 6), ((8, 1), None, None), None))
得到如下所示的特征空间和kd树:
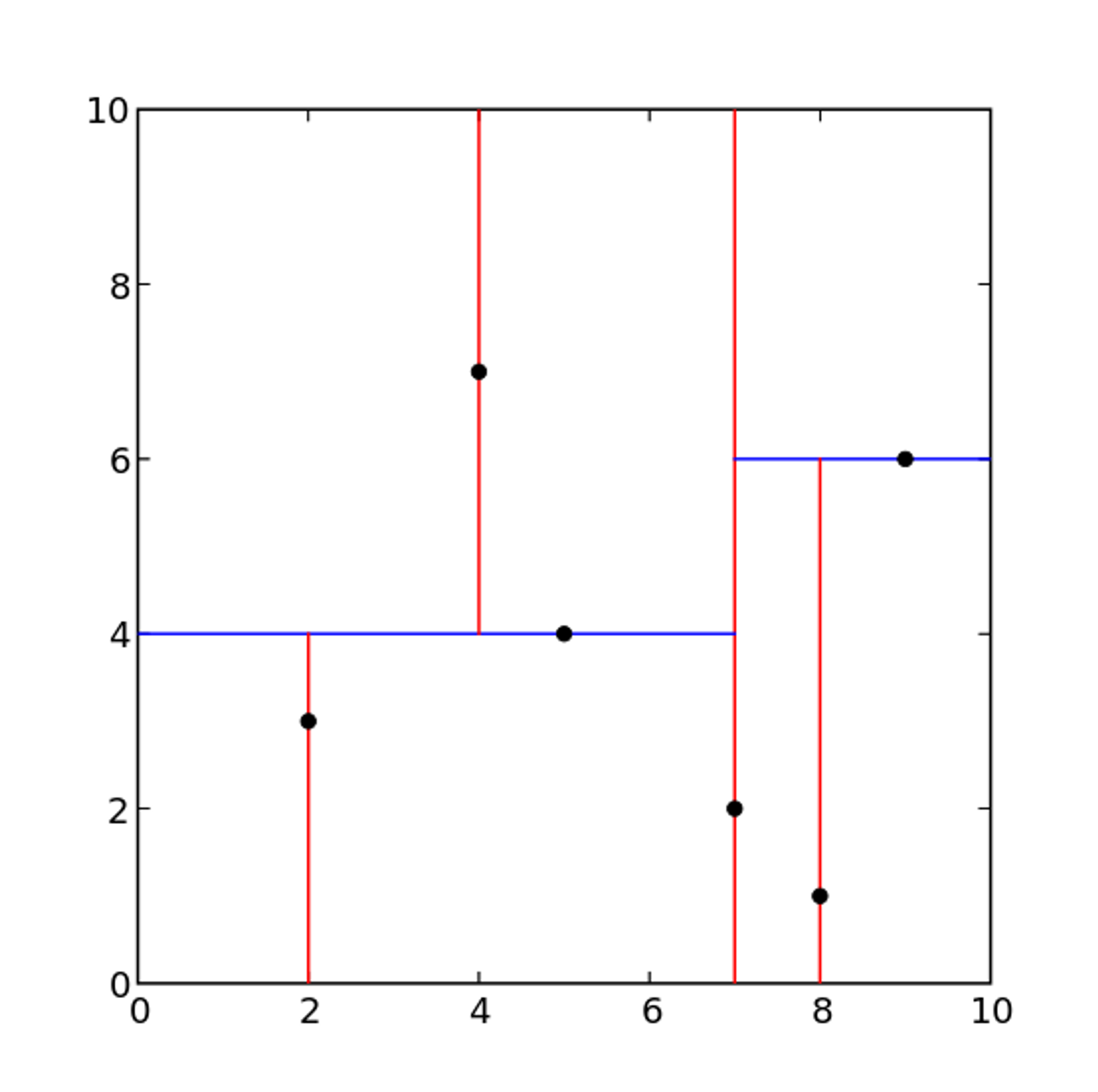
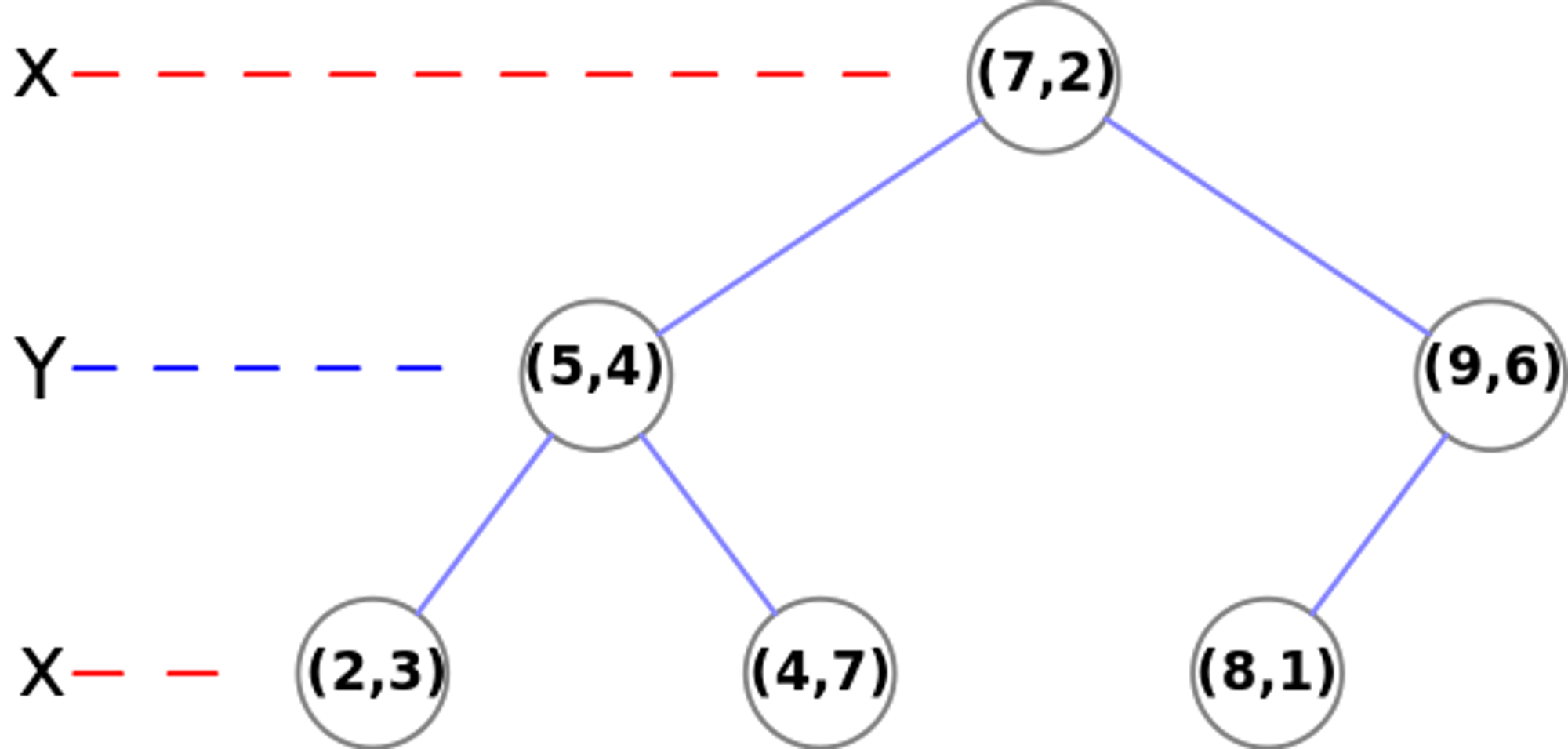
搜索kd树
给定一个目标点,搜索其最近邻,首先找到包含目标点的叶节点,然后从该叶节点出发,依次退回到其父节点,不断查找是否存在比当前最近点更近的点,直到退回到根节点时终止,获得目标点的最近邻点。
算法 (用kd树的最近邻搜索)
输入:已构造的kd树;目标点\\(x\\);
输出:\\(x\\)的最近邻。
(1) 首先找到包含目标节点的叶子结点:从根节点出发,按照相应维度比较,递归向下访问kd树,如果目标点x的当前维度的坐标小于根节点,则移动到左子节点,否则移动到右子节点,直到子节点为叶子节点为止。
(2) 以此叶节点为“当前最近点”
(3) 递归的向上回退,在每个节点进行以下操作:
(a) 如果该节点保存的实例点距离比当前最近点更小,则该点作为新的“当前最近点”
(b) 检查“当前最近点”的父节点的另一子节点对应的区域是否存在更近的点,如果存在,则移动到该点,接着,递归地进行最近邻搜索。如果不存在,则继续向上回退
(4) 当回到根节点时,搜索结束,获得最近邻点
kd树最近邻搜索实现,Python代码如下:
def get_distance(a, b): return np.linalg.norm(a-b) def nn_search(test_point, node, best_point, best_dist, best_label): if node is not None: cur_dist = get_distance(test_point, node.node_feature) if cur_dist < best_dist: best_dist = cur_dist best_point = node.node_feature best_label = node.node_label axis = node.axis search_left = False if test_point[axis] < node.node_feature[axis]: search_left = True best_point, best_dist, best_label = nn_search(test_point, node.left_child, best_point, best_dist, best_label) else: best_point, best_dist, best_label = nn_search(test_point, node.right_child, best_point, best_dist, best_label) if np.abs(node.node_feature[axis] - test_point[axis]) < best_dist: if search_left: best_point, best_dist, best_label = nn_search(test_point, node.right_child, best_point, best_dist, best_label) else: best_point, best_dist, best_label = nn_search(test_point, node.left_child, best_point, best_dist, best_label) return best_point, best_dist, best_label def nn(test_point, tree): best_point , best_dist, best_label = nn_search(test_point, tree, None, np.inf, None) return best_label
小结
KNN是一种lazy-learning算法,它不需要训练,分类的时间复杂度为N(训练样本的个数),引入kd树来实现KNN时间复杂度为logN。kd树更适合于训练样本树远大于空间维度的情况,如果训练样本数接近于空间维度,那么它的效率会迅速下降,几乎接近于线性扫描。
KNN算法不仅可以用于分类,还可以用于回归。
参考文章
- Author:Quanfita
- URL:https://quanfita.cn/article%2Fknn
- Copyright:All articles in this blog, except for special statements, adopt BY-NC-SA agreement. Please indicate the source!
Relate Posts
